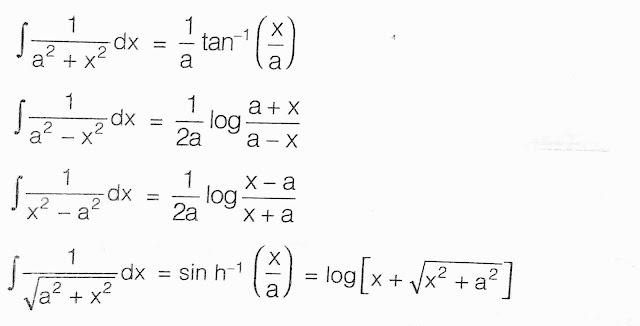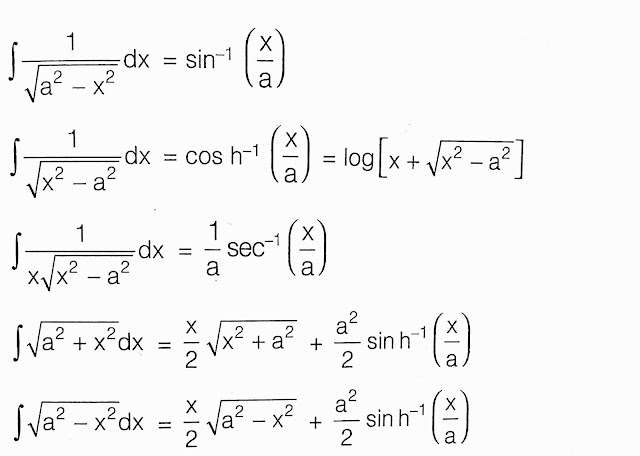Integral
The integral of the product of a constant and a function is equal to be product of the constant and the integral of the function
The integral or sum of aur differentiation of a finite number of function is equal to sum or difference of integrals
Integration of Trigonometric Functions Formulas
- ∫sin x dx = -cos x
- ∫cos x dx = sin x
- ∫tan x dx = ln|sec x|
- ∫sec x dx = ln|tan x + sec x|
- ∫cosec x dx = ln|cosec x – cot x| + C = ln|tan(x/2)|
- ∫cot x dx = ln[sin x|
- ∫sec2x dx = tan x
- ∫cosec2x dx = -cot x
- ∫sec x tan x dx = sec x
- ∫cosec x cot x dx = -cosec x
- ∫sin ax dx = -(cos ax/a)
- ∫cos ax dx = (sin ax/a)
Method of integration
There are variable method of integration by which we can reduce the given integral to one of the known standard integral.
Integration by substitution
A change in the variable of integration often reduce an integral to one of fundamental integrals
Some important formulae based on the above form
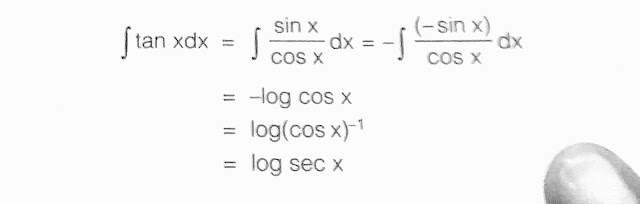
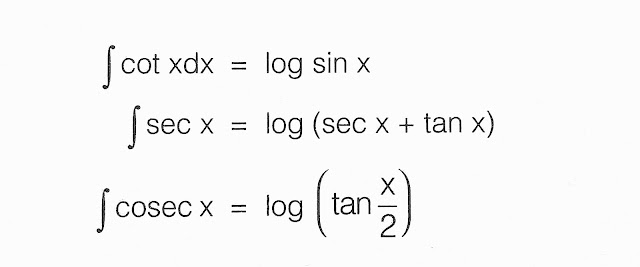
If the integrated consists of the product of a constant power power of a function f(x) and the derivative f'(x) of f(x), to obtain the integral will increase the index by unity and then divide by increased index. This is known power formula.
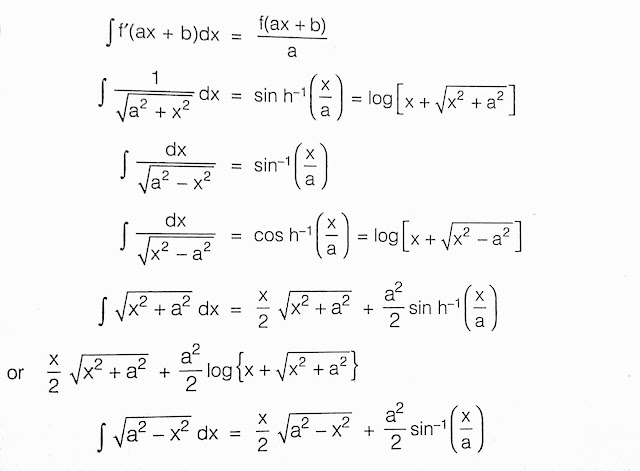
Integral of the product off to function
Integration by part
Formula base upon about method
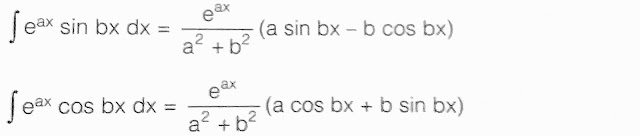
The following is a summary of some of the integrals derived so far by using the three method of integration