सरल आवर्त गति (Simple Harmonic Motion) क्या है
एक निश्चित पथ पर गति करती वस्तु जब एक निश्चित समय अन्तराल के पश्चात् बार-बार अपनी पूर्व गति को दोहराती है, तो इस प्रकार की गति को आवर्त गति कहते हैं तथा यह समयान्तराल आवर्तकाल कहलाता है। जैसे-
(i) पृथ्वी के सूर्य के चारों ओर घूमना आवर्ती गति है, जिसमें आवर्तकाल का मान 1 वर्ष है।
(ii) पृथ्वी का अपने अक्ष के चारों ओर घूमना आवर्ती गति है, जिसमें आवर्त काल का मान 24 घंटे है।
(iii) चन्द्रमा का पृथ्वी के चारों ओर घूमना आवर्ती गति है, जिसमें आवर्त काल का मान 27.3 दिन है।
(iv) घड़ी की सूईयों की गति आवर्ती गति है, जिसमें घण्टे, मिनट व सेकण्ड वाली सूईयों का आवर्तमान 12 घंटे, 60 मिनट एवं 60 सेकण्ड है।
सरल लोलक (Simple Pendulum)
जब एक भार हीन, अवितान्य (भार के कारण न फैलने वाला) और प्रत्यास्थ धागे द्वारा किसी दृढ़ आधार से लटकाया गया भारी कण, जब घर्षणहीन दोलन करता है, तो इस व्यवस्था को सरल लोलक कहते हैं
निलंबन बिंदु (Point of Suspension)
दृढ़ आधार के जिस बिन्दु से लोलक को लटकाया जाता है उसे निलंबन बिन्दु कहते हैं।
लोलक की लम्बाई (Length of Pendulum)
निलम्बन बिन्दु से लोलक के गुरुत्व केन्द्र के बीच की दूरी को लोलक की लम्बाई या प्रभावी लम्बाई कहते हैं। इसे l द्वारा सूचित किया जाता है।
आयाम (Amplitude)
लोलक के गोलक का माध्य स्थिति से किसी भी एक तरफ अधिकतम विस्थापन को दोलन का आयाम कहते हैं।
आयाम = माध्य स्थिति से विस्थापन=x
दोलन गति (Oscillatory Motion)
आवर्त गति में यदि कोई वस्तु एक निश्चित पथ पर एक स्थिर बिन्दु के इर्द-गिर्द गति करती है, तो इसे दोलन गति या कम्पनिक गति कहते हैं।
Ex.: (i) झूला झूलती स्त्री की गति ।
(ii) स्वरित्र द्विभुज की भुजाओं की गति ।
(iii) सरल लोलक की गति ।
सरल आवर्त गति (Simple Harmonic Motion)
किसी सरल रेखीय पथ पर किसी मध्यमान बिन्छु के इर्द-गिर्द ऐसी गति सरल आवर्त गति कही जाती है, जिसका त्वरण सदा मध्यमान बिन्दु की ओर दिष्ट होता है।मध्यमान बिन्दु से विस्थापन के समानुपाती होता है।सभी सरल आवर्त गतियाँ आवर्ती गति होती है लेकिन सभी आवर्ती गतियाँ सरल आवर्त गति नहीं होती है।
सरल आवर्त गति का समीकरण (Equation of SHM)–
यदि किसी क्षण कण की साम्य स्थिति से, विस्थापन y हो, तो
विस्थापन (Y) = Asinot( जहाँA→ आयाम, w→ कोणीय वेग
सरल आवर्त गति का लक्षण (Characteristics of Simple HarmonicMotion)–
(i) त्वरण या प्रत्यानयन बल सदैव माध्य स्थिति की ओर ही लगता है।
(ii) त्वरण या प्रत्यानयन बल सदैव विस्थापन के समानुपाती होता है।
(iii) यह एक बिन्दु के इधर-उधर होती है।
सरल आवर्त गति की विशेषता-
सरल आवर्त गति करने वाला कण जब अपनी माध्य स्थिति से गुजरता है, तो-
(i) उसका त्वरण तथा स्थितिज ऊर्जा शून्य होती है।
(ii) कोई बल कार्य नहीं करता
(iii) वेग तथा गतिज ऊर्जा अधिकतम होती है।
सरल आवर्त गति करने वाला कण जब अपनी गति के अन्त: बिन्दुओं से गुजरता है-
(i) इसमें त्वरण तथा स्थितिज ऊर्जा अधिकतम होती है।
(ii) इसमें प्रत्यानयन बल कार्य करता है।
(iii) वेग तथा गतिज ऊर्जा शून्य होती है।
एक दोलन या एक कम्पन
दोलन करने वाले कण का अपनी साम्य स्थिति के एक और जाना फिर साम्य स्थिति में आकर दूसरी ओर जाना और पुनः साम्य स्थिति में वापस लौटना एक दोलन या कम्पन कहलाता है।
आवृत्ति (Frequency)
कम्पन करने वाली वस्तु एक सेकण्ड में जितना कम्पन करती है, उसे उसकी आवृत्ति कहते हैं। इसका SI मात्रक हर्ट्ज होता है। यदि आवृत्ति n तथा आवर्तकाल T हो, तो होता है।
आवर्त काल (Time Period)
एक दोलन पूरा करने में लगे समय को आवर्तकाल कहते हैं। कम्पन गति के आवर्त काल को कम्पन काल या दोलन काल भी कहते हैं। इसे T द्वारा सूचति करते हैं। T= से.
कोणीय आवृत्ति (Angular Frequency)
राशि से आवृत्ति (n) के गुणन को कोणीय आवृत्ति कहा जाता है। इसे w से सूचित किया जाता है।
कोणीय आवृत्ति w = 2πn
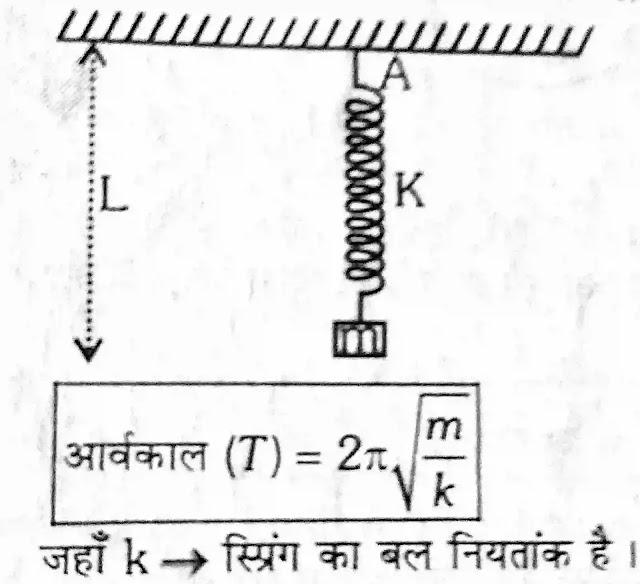
स्प्रिंग में लड़के पिंड की गति (Motion of a body suspended by a string)
माना कि एक हल्की स्प्रिंग जिसकी सामान्य लंबाई ‘L’ है, एक दृढ़ आधार A से लटकी है। यदि m द्रव्यमान के पिंड को स्प्रिंग के निचले सिरे से लटकाकर और थोड़ा खींचकर छोड़ दिया जाए तो वह ऊपर-नीचे दोलन करने लगता है, जिनका-
सरल लोलक (Simple Pendulum):
यदि किसी डोरी का एक सिरा किसी दृढ़ आधार से बँधा हो और उसके दूसरे सिरे पर कोई भारी वस्तु लटकी हो, जो ऊर्ध्वाधर तल में स्वतंत्रतापूर्वक दोलन करता हो, तो ऐसे प्रबंध को सरल लोलक कहते हैं। डोरी हल्की, प्रत्यास्थ (Elastic) और भार के कारण लंबाई न बढ़ने वाली होनी चाहिए। भारी वस्तु प्रायः धातु का कोई छोटा गोला होता है। इसे गोलक अथवा लोलक (Bob) कहते हैं।
लोलक की लंबाई (Length of Bob)
लटकन बिंदु O से गोलक के केन्द्र के बीच की दूरी को लोलक की लंबाई कहते हैं | OC लोलक की लंबाई है।
आयाम (Amplitude)
दोलन करते गोलक की माध्य स्थिति में दोनों ओर तय की गयी अधिकतम लंबाई या कोणीय विस्थापन (Angular displacement) को आयाम कहते हैं।
पूर्ण दोलन (Complex Oscillation) –
एक दूरतम स्थिति (Ex- treme Position) A से दूसरी दूरतम स्थिति B और वापस A तक की गति को एक पूर्ण दोलन कहते हैं।
आवर्तकाल (Time period)
एक पूर्ण दोलन में लगे समय को आवर्तकाल अथवा ‘दोलनकाल’ कहते हैं।
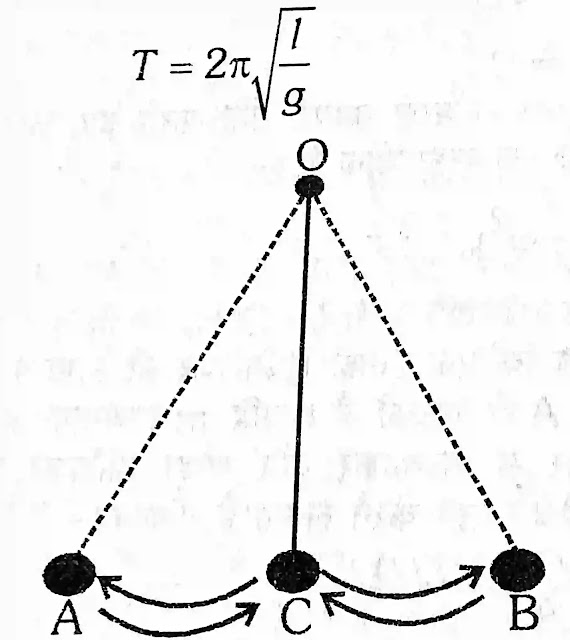
जहाँ T = आवर्तकाल, l = लोलक की लंबाई, g= गुरुत्वीय त्वरण
आवृत्ति संख्या (Frequency Number)
एक सेकेंड में लोलक द्वारा किए गए पूर्ण दोलनों की संख्या को ‘आवृत्ति संख्या’ कहते हैं। bl sn से सूचित करते हैं।
दोलन के नियम (Laws of Oscillation)
समकाल का नियम (Law of Isochronium)
इस नियम के अनुसार, आयाम का मान भिन्न रहने पर भी लोलक की लंबाई समान रहने पर उसका दोलनकाल समान होता है।
मात्रा का नियम (Lawof Mass)
लोलक की लंबाई समान रहने पर लोलक का दोलनकाल उसकी मात्रा, आकार तथा प्रकृति पर निर्भर नहीं करता है।
लंबाई का नियम (Law of lenght)
लोलक का दोलनकाल उसकी लंबाई के वर्गमूल के अनुक्रमानुपाती होता है।
गुरुत्वीय त्वरण (g) का प्रभाव (Effect of g)–
• लोलक का दोलनकाल उस स्थान के गुरुत्वीय त्वरण के वर्गमूल के व्युत्क्रमानुपाती होता है।सरल लोलक के सूत्र से निम्न निष्कर्ष निकलता है-
• इसी कारण कोई लड़की झूला झूलते खड़ी हो जाए तो उसका गुरुत्व केन्द्र ऊपर उठ जाएगा और प्रभावी लम्बाई घट जाएगी जिससे झूले का आवर्तकाल घट जाएगा। अतः झूला जल्दी-जल्दी दोलन करेगा।
• यानि किसी लोलक घड़ी को पृथ्वी तल से ऊपर या
नीचे ले जाया जाए तो घड़ी का आवर्तकाल बढ़ जाएगा। अतः घड़ी सुस्त हो जाती है, क्योंकि पृथ्वी तल से ऊपर या नीचे जाने पर g का मान घटता है।
• चंद्रमा पर लोलक घड़ी को ले जाने पर उसका आवर्तकाल बढ़ जायेगा क्योंकि चंद्रमा पर g का मान पृथ्वी के g के मान का 1/6 गुना है ।