त्रिभुज (Triangley )
तीन भुजाओं से घिरा हुआ आकृति त्रिभुज कहलाता है। इसमें तीन कोण होते है
सामान्य परंपरा (General Convention)
i) भुजाओं, शीर्ष और कोणों का नामकरण सामान्यत: clockwise दिशा क़म में किया जाता है।
ii) शोर्थ A के सम्मुख की भुजा को a शीर्ष b के सम्मुख को भुजा को b इत्यादि लिखा है।
iii) कोण A (या कोण BAC) को.कोण A (या कोण BAC) लिखा जाता है और यह कोण शीर्ष A पर स्थित भुजाएँ b और c से अंतरित होता है। यह भुजा a के सम्मुख होता है। इसी तरह हम कोण B और कोण C को भी लिख सकते है।
त्रिभुज के तीनों कोणों का योग 180⁰ के बराबर होता है। इसतरह, जिसकी कोण A+B+C-180⁰
(a) त्रिभुज का क्षेत्रफल, A = 1/2 (आधार×ऊंचाई) = 1/2×bh
(b) b = 2A/h.
वैकल्पिक विधि : हम लिख सकते हैं,
क्षेत्रफल = 1/2×ah
जहाँ h ,शीर्ष A से भुजा ‘a’ पर डाली गई लंव की लंबाई इसी तरह, हम भुजा और उस पर शीर्ष से खोंचे गये लंब को लेकर भी सूत्र लिख सकते हैं।
2.∆ABC का क्षेत्रफल
(A) = √S(S-a)(s-b)(s-c)
जहाँ, s त्रिभुज की अर्द्ध-परिमिति है और, S =1/2× (a+b+c)
P=a+b+c = 2S
समकोण त्रिभुज (Right Angled Triangle) :
यह एक ऐसा त्रिभुज जिसका एक कोण समकोण अर्थात् (90) है।
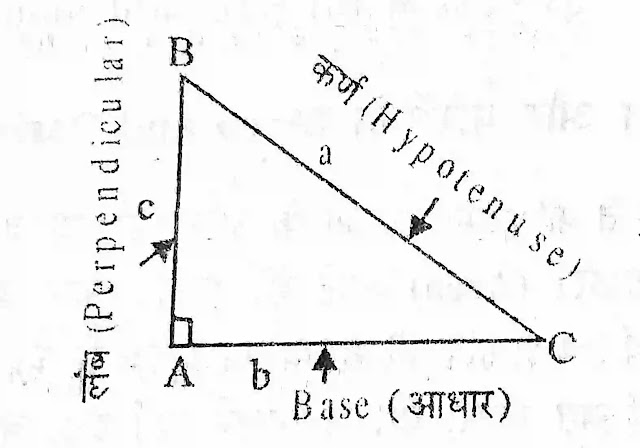
कोण A =90⁰
कोणB + कोणC = 90⁰
a² = b² + c²(पाइथागोरस प्रमेय)
A = 1/2×bc
समद्विबाहु त्रिभुज (Isosceles Triangle) :
यह ऐसा त्रिभुज है जिसको दो भुजाएँ बराबर होती हैं। यह भी साबित किया जा सकता है कि ऐसे त्रिभुज में बराबर भुजाओं के सम्मुख वाले कोण भी बराबर होंगे। इस तरह इसमें दो कोण भी बराबर होते हैं।
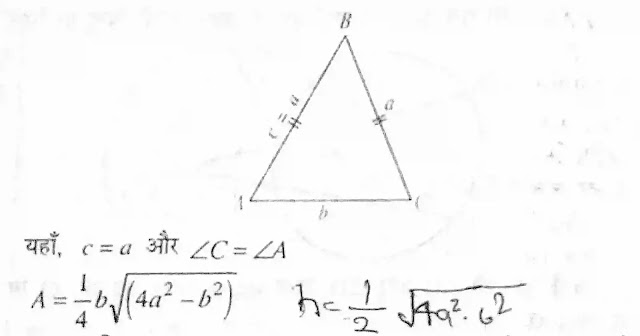
समबाहु त्रिभुज
यह एक ऐसा त्रिभुज है जिसकी तीनो भुजा आपस में बराबर होती है यह भी साबित किया जा सकता है कि इसके तीनों कोण भी बराबर होते हैं और प्रत्येेक कोण का मान 60⁰ होता है
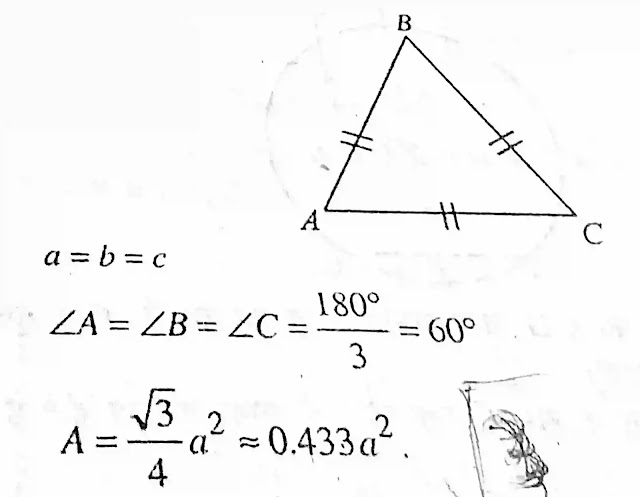
समदिबाहु त्रिभुज
यह एकत ऐसा समदिबाहु त्रिभुज है जिसमें दो समान भुजाओं के बीच का कोण 90 डिग्री है दूसरे शब्दों में हम इस तरह भी कह सकते हैं कि यह एक ऐसा समकोण त्रिभुज है जिसमें लंब और आधार की भुजा बराबर हो
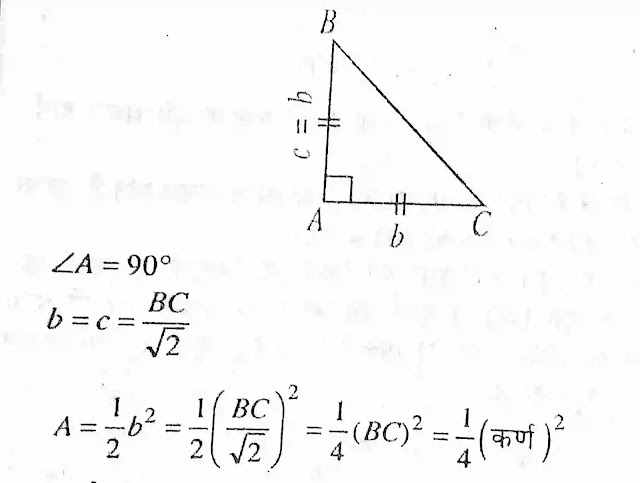
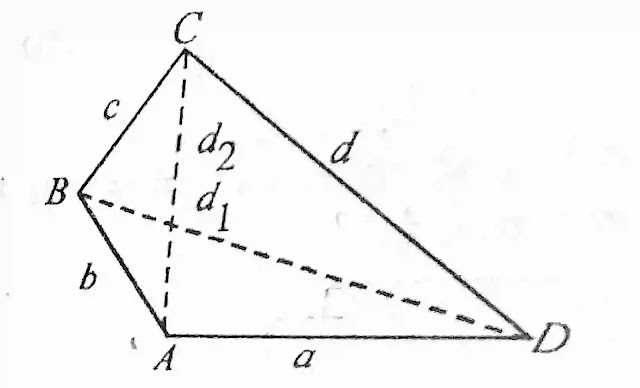
चतुर्भुज
चार भुजा उनमें से गिरा हुई आकृति चतुर्भुज कहलाती है इसमें चार कोण होते हैं चारों कोणों का योग 380 डिग्री होता है
वर्ग (Square)
इसकी सभी भुजाएं आपस में बराबर होती है और प्रत्येक कोण समकोण होते हैं इसके विकणऀ बराबर होते हैं और एक दूसरे को 90⁰ पर समदिभाषित करते हैं
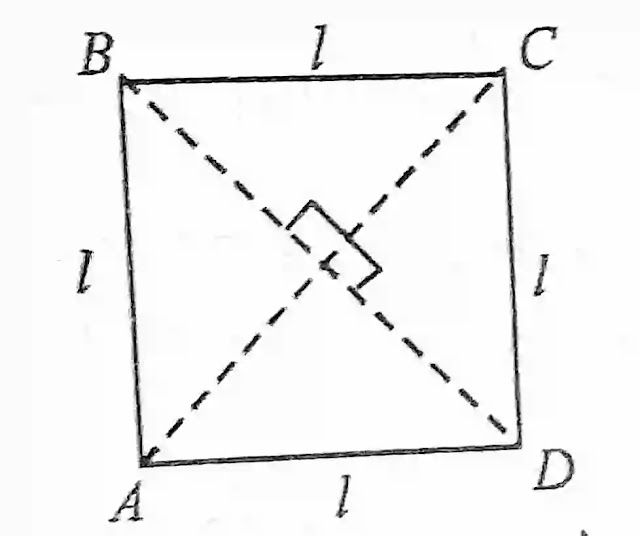
क्षेत्रफल =l² प्रत्येक l भुजा की लंबाई है
AC =BD =√2l
l =1/√2×(विकणृ) = d/√2
इसलिए हम लिख सकते हैं
A = l² =d²/2
P =4l
आयत (Rectangle)
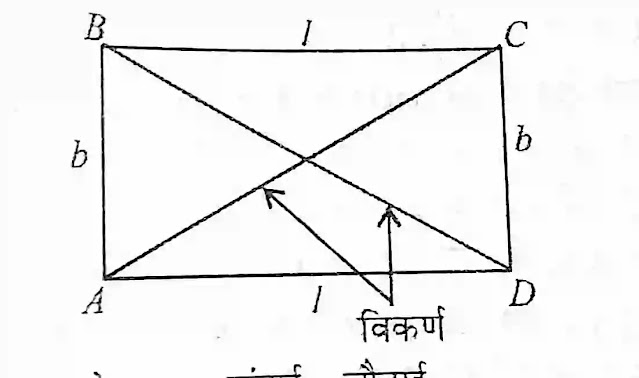
एक ऐसा चतुर्भुज है जिसका प्रत्येक कोण 90 डिग्री का होता है और आमने सामने की भुजा समांतर और बराबर होती है इसके विकर्ण बराबर होते हैं तथा एक दूसरे को समदिभाजित करते हैं।
आयत का क्षेत्रफल = लंबाई × चौड़ाई
(I) A =lb
(II) l =A/b
(III) b =A/l
विकर्ण AC=BD=√l²+b²
P=2(l+b)
समानांतर चतुर्भुज (Parallelogram)
ऐसा चतुर्भुज जिसके आमने-सामने की भुजाओं का योग में समान तथा समानांतर होता है समानांतर चतुर्भुज करते हैं
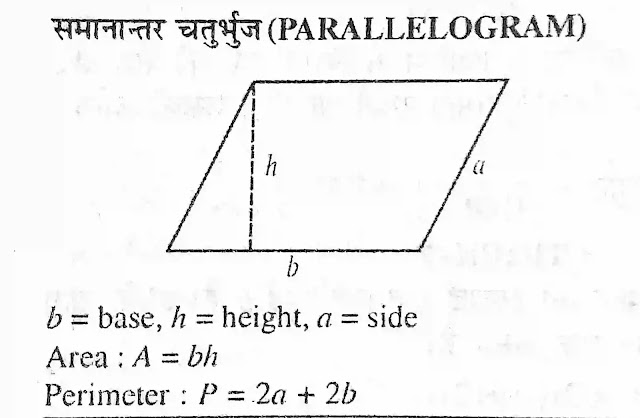
क्षेत्रफल- आधार x अंचाई
या,A =lb
और,P=2(l+b)
इसका प्रत्येक विकर्ण, चतुर्भुज को दो बराबर भागों में बाँटता है।
समचतुर्भुज (Rhombus) :
यह एक ऐसा समानांतर चतुर्भुज है जिसकी का चारों भुजाएँ बराबर होती हैं।
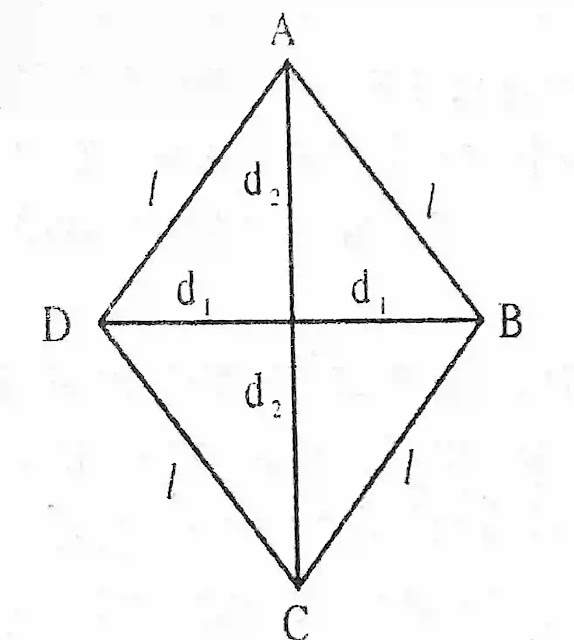
इसके विकर्ण एक-दूसरे को 90° पर समद्विभाजित करते हैं।इसके सम्मुख कोण समान होते हैं।
क्षेत्रफल = 1/2× (विकणों की लंबाई का गुणनफल)
परिमिति (P) =4l
समलंब चतुर्भुज (Trapezium) :
ऐसा चतुर्भुज जिसके आमने-सामने के भुजाओं का केवल एक युग्म समानांतर होता है, समलंब चतुर्भुज कहलाता है।
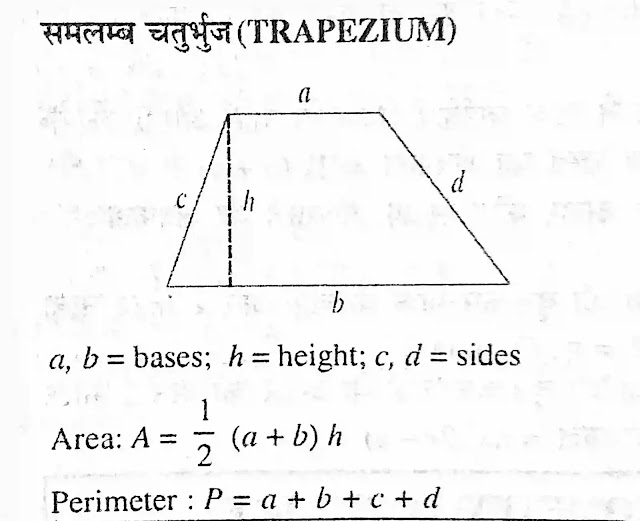
यहाँ BC और AD समानांतर हैं।
क्षेत्रफल =1/2× (समानांतर भुजाओं का योग) x (उनके बीच की दूरी अर्थात् ऊँचाई)
A = 1/2 ×(a + b)xh
P =a+b+c+d.
नोट : समलंब चतुर्भुज के समानांतर भुजाओं के बीच की दूरी को इसकी ऊँचाई कहते हैं।
वृत्त (Circle) :
वृत्त एक ऐसा बिंदुपथ है जिसकी दूरी एक नियत बिंदु से हमेशा समान होती है। यह नियत बिंदु वृत्त का केंद्र कहलाता है और केंद्र से इसकी दूरी त्रिज्या कहलाती है।
.वृत्त में प्रयोग होने वाले शब्द
परिधि (Circumference): वृतको भरने वाली रेखा परिधि कहलाती है।
त्रिज्या (Radius) : केंद्र से परिधि तक की दूरी को निभ्या कहा जाता है। एक वृत्त में अनन्त क्रियाएँ होती है तथा सभी त्रिज्या आपस में समान होगी हैं।
केन्द्र (Centre) : वृक्ष के अंदर कॉट वह बिंदु होता है, जहाँ से किसी वृत्त की परिधि समान दूरी पर होती है।
व्यास (Diameter): एक ऐसी रेखा जो केंद्र से होकर गुजरती है तथा दोनों तरफ परिधि से मिलती है, व्यास कहलाता है। एक वृत्त के अंदर अनन्त व्यास खींची जा सकती है तथा खींचे गए सभी व्यास की लंबाई समान होती है।
जीवा (Chord) : ऐसी रेखा से दोनों तरफ परिधि से मिलती है, परंतु केंद्र से होकर नहीं गुजरती है, जीया कहलाती है।
वृत्त चाप (Are) : वृत्त की परिधि पर स्थित दो बिंदु की लंबाई (चक्र में) वृत्तचाप कहलाता है। यह वृत की परिधि का एक भाग होता है।

प्रयोग होने वाले प्रमुख सूत्र :
क्षेत्रफल, A =πr²=π/4×D² जहाँ -π =22/7 = 3.14
जिसकी
और, व्यास,D-2r
परिधि P=2πr =πD
D =P/π
हम यह भी लिख सकते हैं,A =P²/4π
P = √4πA
एक वृत्त में कुल अंतरित कोण 360″ होता है।
वृत चाप (Arc)
वृत्त चाप ACB की लंबाई =(थीफ/360°)×2πr(जहाँ थीठ बहुत छोटा हो)
जहाँ थीठ – वृत्त चाप का कोण है।
या, वृत्त चाप ACB- -ं थीठ/360°X परिधि
त्रिग्यखंड (Sector) :
वृत्त चाप, उनके दो त्रिज्याएँ और केंद्र के बीच अंतरित क्षेत्र वृत्त का त्रिज्याखंड कहलाता है। दूसरे शब्दों में, वृत्त के केंद्र को एक चाप के सिरों से मिलने वाली त्रिज्याओं एवं चाप के बीच के क्षेत्र को त्रिपखंड कहते हैं।
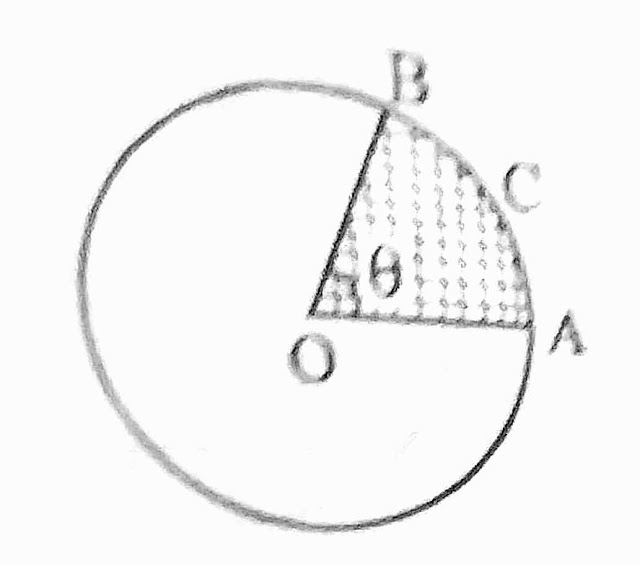
यहाँ क्षेत्र AOBCA वृत्त चाप ACB से घिरा क्रिज्यखंड है। इसे सामान्यतः त्रिज्याखंड AOD भी कहा जाता है।
त्रिज्याखंड AOB का क्षेत्रफल
=(थीफ/360°)×πr²
कमरा (Room): कमरे की एक लबाई, चौड़ाई (b) और ऊँचाई होती है।
कमरे के चारों दीवारों का क्षेत्रफल = 2h(l+b)
समान कमरे के फर्श और चारों दीवारों का क्षेत्रफल =2h(l+b)+lb
कमर के फर्श, छा और चरों रोकारों का क्षेत्रफल -2[h(l+b)+lb]
बहुभुज क्षेत्र (Polygon) :
अनेक भुजाओं से घिरी हुई आकृति/क्षेत्र को बहुभुजक्षेत्र (polyson) कहा जाता है। सामान्यतः इसका प्रयोग चार सेश्रअधिक भुजाओं वाली आकृति के लिए किया जाता है। उदाहरणार्थ, पंचभुज क्षेत्र (pentagI), षटभुज क्षेत्र (hexagon) इत्यादि।
समबहुभुर क्षेत्र (Regular Pulygon) : यह एक ऐसा बहुभुत क्षेत्र है जिसकी सभी भुजाएँ, समान होती हैं।
अंत:वृत्त (Incircle or Insribed Circle) :
अनुभुज क्षेत्र के अंदर ऐसो वृत्त जो उसर्व सभी भुजाओं को स्पर्श कर रही हो, उसे अंत:वर कहते हैं।
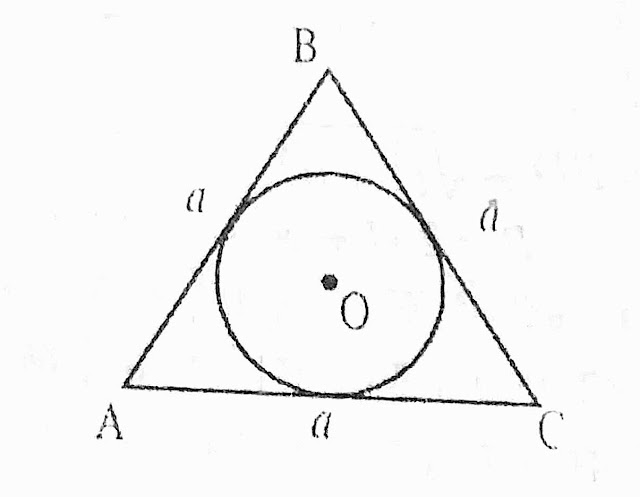
‘a’ भुजा वाली समचार त्रिभुज में अंत:वृत्त की त्रिज्या = a/2√3
परिवृत्त (Circumcirele) :
ऐसा जिसकी परिधि बहुभुज क्षेत्र के सभी शौर्षों को स्पर्श कर रही हो, उसे परिवृत्त कहते हैं।
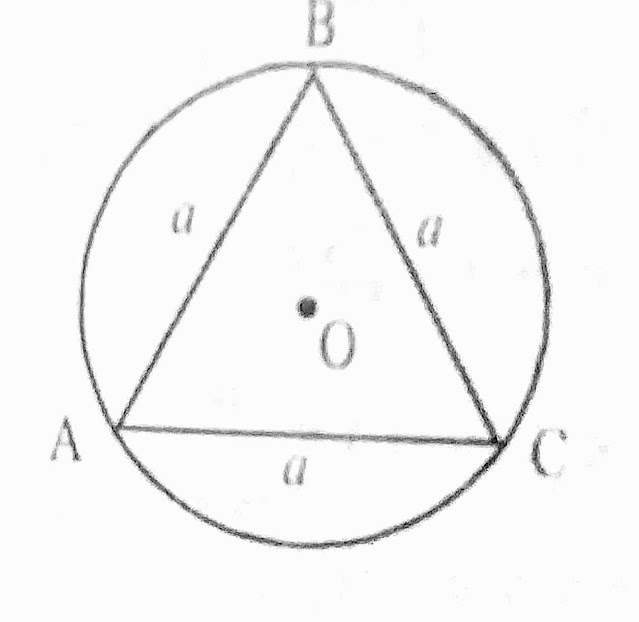
भुजावाली समबाहु त्रिभुज के लिए परिवृत्त की परित्रिज्या = a/√3
समबहुभुज क्षेत्र का क्षेत्रफल =
1/2 x (भुजाओं की संख्या)x (अंत:वृत की अंत:त्रिज्या)
षट्क्षेत्र का क्षेत्रफल = 3√3/2 (भुजा)² = 2.598 ( भुजा)²
सम अष्टभुजक्षेत्र का क्षेत्रफल = 2[√2 + 1) (भुजा)² =4.828 (भुजा)²
चक्रीय चतुर्भुज
ऐसा चतुर्भुज जिसके सभी शीर्ष व्रत की परिधि पर होते हैं उसे चक्रीय चतुर्भुज कहते हैं

घनाभ
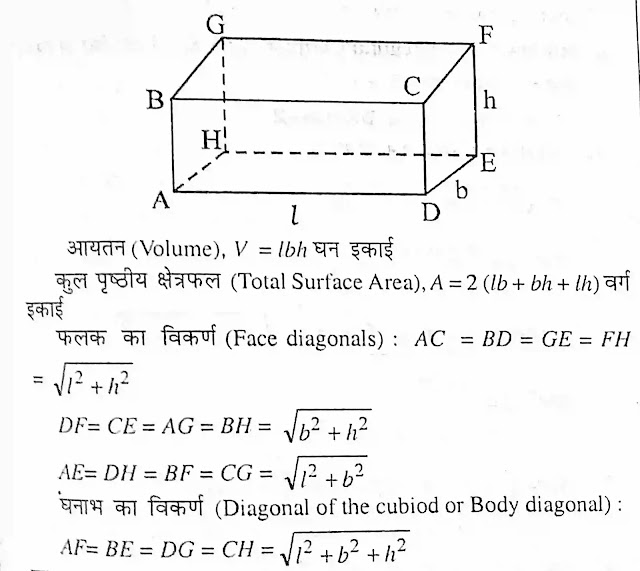
घनाभ में छः आयताकार फलन होते हैं जिसकी सभी भुजाएं/ किनारों/ फलको का मिलान समकोण पर होता है सम्मुख फलको का युग्म में समान होता है
घन
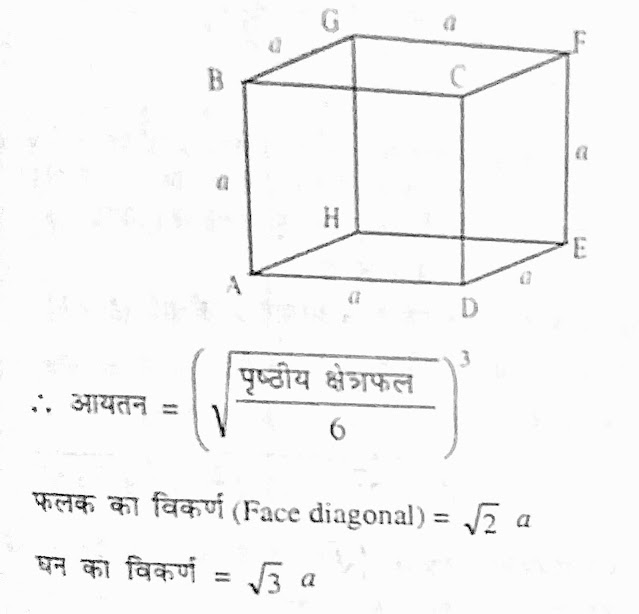
घन घनाभ की एक विशेष स्थिति है जिसमें l=b=h=c
आयतन = a³ घन ईकाई
कुल पृष्ठीय क्षेत्रफल = 6a²वर्ग ईकाई
बेलन (Cylinder)

एक आयत को उसकी एक भुजा के परित चारों तरफ घुमाने पर प्राप्त त्रिविमोच आकृति बेला होता है।
r- बेलन की त्रिज्या
h- बेलन की ऊँचाई या लंबाई
यहाँ, ABCD बेलन को उत्पन करने वाला आया है।
आयतन =πr²h
वक पृष्ठ का क्षेत्रफल-2πr²h वर्ग इकाई
संपूर्ण या कुल पृष्ठीय क्षेत्रफल – 2πr(h + r) वर्गका
गोला (Sphere)
r- गोला की त्रिज्या
आयतन =4/3×πr³
पृष्ठीय क्षेत्रफल – 4πr² वर्ग इकाई
खोखला गोला (Hollow Sphere)
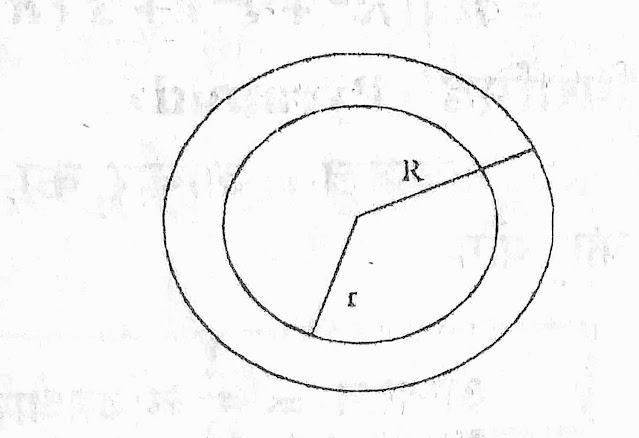
आन्तरिक पृष्ठ क्षेत्रफल – 4πr²
बाह्य पृष्ठ क्षेत्रफल – 4πR²
आयतन: 4/3π[R³-r³]
अर्द्धगोला (Hemisphere)
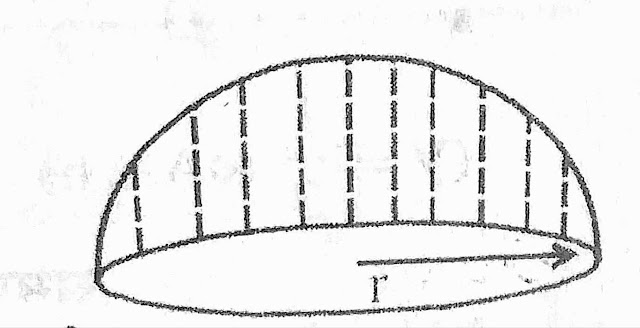
आयतन = 2/3πr³
चक्र पृष्ठों का क्षेत्रफल – 2πr² वर्ग इकाई
कुल पृष्टीय क्षेत्रफल – 3πr²वर्ग इकाई
शंकु (लंब वृत्तीय शंकु ) (Cone)
एक समकोण त्रिभुज को इसके ऊचाई के परित घुमाने से पनी त्रिवीमीय आकृति शंकु होती है।
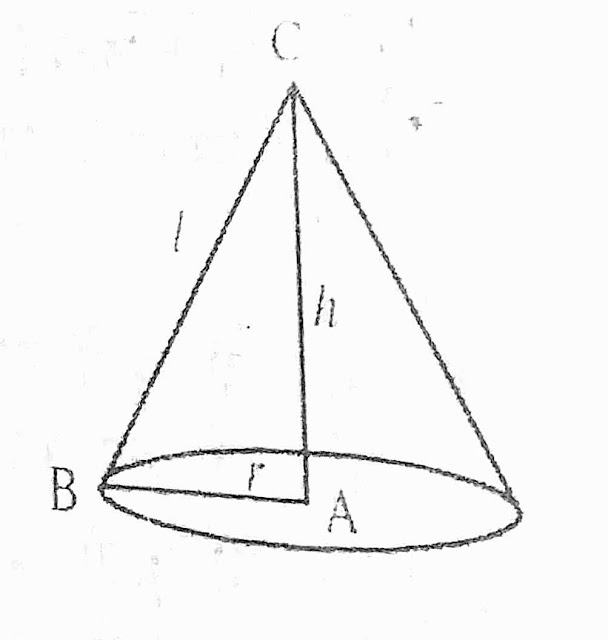
आयतन =1/3×πr²h
वक पृष्ठ का क्षेत्रफल-πr²l वर्ग इकाई
आधार का क्षेत्रफल-πr²
संपूर्ण या कुल पृष्ठीय क्षेत्रफल -πr(l+r)